
Turinys:
- Autorius Miles Stephen [email protected].
- Public 2023-12-15 23:38.
- Paskutinį kartą keistas 2025-01-22 17:04.
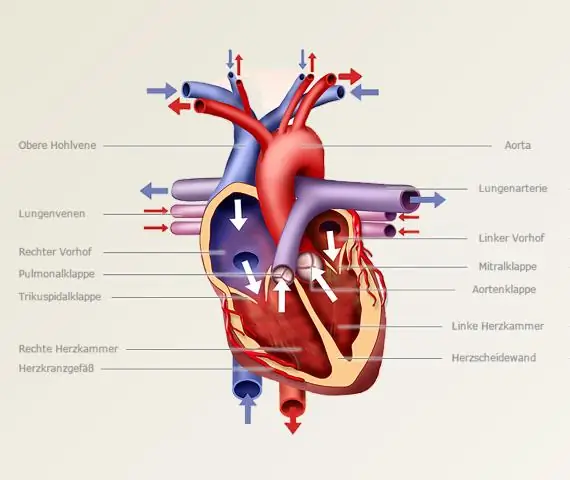
Netiesinė regresija gali tinka daugeliui kitų kreivių tipų, bet tai gali reikia daugiau pastangų, kad būtų galima rasti tinkamiausią ir interpretuoti nepriklausomų kintamųjų vaidmuo. Be to, R kvadratas negalioja netiesinė regresija , ir to padaryti neįmanoma apskaičiuoti parametrų įverčių p reikšmės.
Ar tokiu būdu regresija gali būti netiesinė?
Statistikoje, netiesinė regresija yra forma regresija analizė, kurioje stebėjimo duomenys modeliuojami funkcija, kuri yra a netiesinis modelio parametrų derinys ir priklauso nuo vieno ar kelių nepriklausomų kintamųjų. Duomenys suderinami nuoseklių aproksimacijų metodu.
Taip pat galima paklausti, ar r kvadratas yra tik tiesinei regresijai? Bendroji matematinė sistema, skirta R - kvadratu neveikia tinkamai, jei regresijos modelis nėra linijinis . Nepaisant šios problemos, dauguma statistikos programinės įrangos vis tiek skaičiuoja R - kvadratu netiesiniams modeliams. Jei naudojate R - kvadratu išsirinkti geriausią modelis , tai veda prie tinkamo tik modelis 28-43% laiko.
Kalbant apie tai, kaip apskaičiuoti netiesinę regresiją?
Jei jūsų modelis naudoja lygtis forma Y = a0 + b1X1, tai yra tiesinė regresija modelis. Jei ne, tai netiesinis.
Y = f(X, β) + ε
- X = p prognozių vektorius,
- β = k parametrų vektorius,
- f(-) = žinoma regresijos funkcija,
- ε = klaidos terminas.
Kokie yra regresijos tipai?
Regresijos tipai
- Tiesinė regresija. Tai paprasčiausia regresijos forma.
- Polinominė regresija. Tai būdas pritaikyti netiesinę lygtį, imant nepriklausomo kintamojo daugianario funkcijas.
- Logistinė regresija.
- Kvantilė regresija.
- Ridžo regresija.
- Lasso regresija.
- Elastinė grynoji regresija.
- Pagrindinių komponentų regresija (PGR)
Rekomenduojamas:
Kokius veiksmus reikia atlikti norint nubraižyti funkciją?
Funkcijos grafiko eskizavimo žingsniai Nustatykite, ar funkcija gaunama transformuojant paprastesnę funkciją, ir atlikite reikiamus veiksmus šiai paprastesnei funkcijai. Nustatykite, ar funkcija yra lyginė, nelyginė ar periodinė. Raskite y pertrauką (tašką). Raskite x pertraukas (taškus, kur). Raskite asimptotų funkciją, jei tokių yra
Kaip atlikti paprastą tęstinumo tikrintuvą?

VIDEO Taip pat kyla klausimas, kas yra paprastas tęstinumo tikrintuvas? A tęstinumo testeris yra paprastas prietaisas, susidedantis iš dviejų bandymo zondų ir šviesos (LED) arba garsinio signalo indikatoriaus. Jis naudojamas aptikti buvimą tęstinumą arba pertrauka tarp dviejų laidininko galų, prijungto prie jo bandymo zondų.
Kaip atlikti sinusoidinę regresiją skaičiuotuvu?
VIDEO Kaip apskaičiuoti sinusoidinę regresiją? Sinusoidinė regresija . Sureguliuokite A, B, C ir D reikšmes lygtis y = A*sin(B(x-C))+D, kad būtų a sinusoidinis kreivė tinka tam tikram atsitiktinai sugeneruotų duomenų rinkiniui. Kai atliksite gerą funkciją, spustelėkite „Rodyti apskaičiuotą“, kad pamatytumėte apskaičiuotą regresija linija.
Kuris duomenų klasifikavimo metodas pateikia vienodą įrašų arba analizės vienetų skaičių kiekvienoje duomenų klasėje?

Kvantilė. kiekvienoje klasėje yra vienodas funkcijų skaičius. Kvantiline klasifikacija gerai tinka tiesiškai paskirstytiems duomenims. Kvantilė kiekvienai klasei priskiria tą patį duomenų reikšmių skaičių
Kuri duomenų charakteristika yra labai vertingo duomenų kiekio matas?
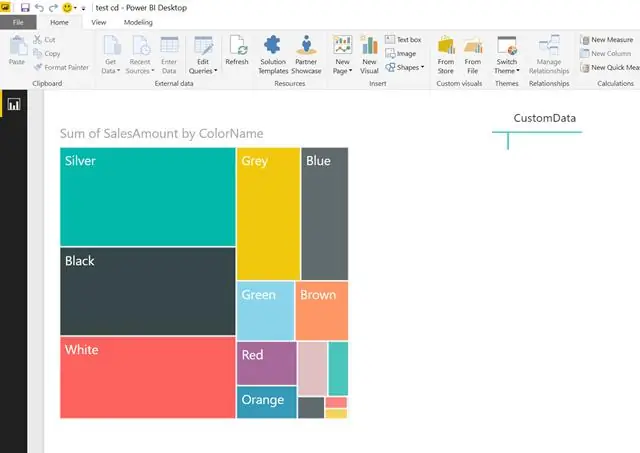
Variantas: dydžio, kuriuo skiriasi duomenų reikšmės, matas. ? Paskirstymas: duomenų sklaidos verčių diapazone pobūdis arba forma (pvz., varpelio formos). ? Išskirtinės vertės: imties reikšmės, kurios yra labai toli nuo daugumos kitų imties verčių
