
Turinys:
- Autorius Miles Stephen [email protected].
- Public 2024-01-18 08:17.
- Paskutinį kartą keistas 2025-06-01 05:05.
Begalinio rinkinio pavyzdžiai:
- Nustatyti visų plokštumos taškų yra an begalinis rinkinys .
- Nustatyti visų linijos atkarpos taškų yra an begalinis rinkinys .
- Nustatyti visų teigiamų sveikųjų skaičių, kuris yra 3 kartotinis, yra an begalinis rinkinys .
- W = {0, 1, 2, 3, ……..} t.y. rinkinys iš visų sveikųjų skaičių yra an begalinis rinkinys .
- N = {1, 2, 3, ……….}
- Z = {………
Panašiai galite paklausti, kaip parodyti begalinį rinkinį?
Galite įrodyti, kad aibė yra begalinė, tiesiog parodydami du dalykus:
- Tam tikram n jis turi bent vieną n ilgio elementą.
- Jei jis turi maksimalaus baigtinio ilgio elementą, tuomet galite sukurti ilgesnį elementą (taip paneigdami, kad maksimalaus baigtinio ilgio elementas).
Antra, kaip atskirti, ar aibė yra begalinė, ar baigtinė? Taškai, norint nustatyti aibę kaip baigtinę ar begalinę, yra:
- Jei aibė turi pradžios ir pabaigos tašką, tada ji yra baigtinė, o jei ji neturi pradžios ar pabaigos taško, tada ji yra begalinė.
- Jei aibėje yra ribotas elementų skaičius, tada ji yra baigtinė, o jei jos elementų skaičius neribotas, tada ji yra begalinė.
Antra, kas yra baigtinis ir begalinis rinkinys su pavyzdžiu?
Pavyzdžiai apie Begaliniai rinkiniai Jeigu rinkinys nėra a baigtinis rinkinys , tada tai yra an begalinis rinkinys . Natūralūs skaičiai ir sveikieji skaičiai yra du pavyzdžių apie rinkiniai tai yra begalinis ir todėl ne baigtinis . Paryškinta didžioji Z raidė dažnai naudojama norint nurodyti rinkinys sveikųjų skaičių.
Ar egzistuoja begalinės aibės?
Nėra begalinės aibės . Ne tik daryti begalinius rinkinius ne egzistuoja , tačiau pati koncepcija logiškai prieštaringa - niekuo nesiskiria nuo „kvadratinių apskritimų“. Begaliniai rinkiniai yra pažodžiui įtraukti į šiuolaikinius matematikos pagrindus - su vadinamąja „aksioma Begalybė ”.
Rekomenduojamas:
Kaip parašyti junginio, kuriame yra poliatominis jonas, formulę?
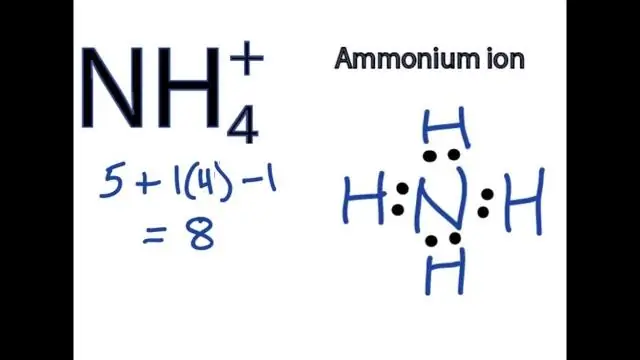
Norėdami parašyti junginių, kurių sudėtyje yra poliatominių jonų, formules, parašykite metalo jono simbolį, po kurio - daugiaatominio jono formulę ir subalansuokite krūvius. Norėdami pavadinti junginį, kuriame yra poliatominis jonas, pirmiausia nurodykite katijoną, o tada anijoną
Kaip išbandyti dirvožemio pH rinkinį?

Į dirvą įpilkite 1/2 puodelio baltojo acto. Jei jis putoja, jūsų dirvožemis yra šarminis, kurio pH yra nuo 7 iki 8. Jei atlikus acto testą jis neputoja, į kitą talpyklą įpilkite distiliuoto vandens, kol 2 arbatiniai šaukšteliai dirvožemio taps dumblūs. Įpilkite 1/2 puodelio kepimo sodos
Kaip parašyti trupmeną kaip sveikojo skaičiaus ir vienetinės trupmenos sandaugą?

Vienetinės trupmenos ir sveikojo skaičiaus sandaugos radimo taisyklės Pirmiausia sveikąjį skaičių užrašome trupmena, t.y., padalijus iš vieneto; pavyzdžiui: 7 rašomas kaip 71. Tada padauginame skaitiklius. Vardiklius padauginame. Jei reikia supaprastinti, tai daroma ir tada rašome galutinę trupmeną
Kaip parašyti dvisąlygas kaip dvi sąlygas?
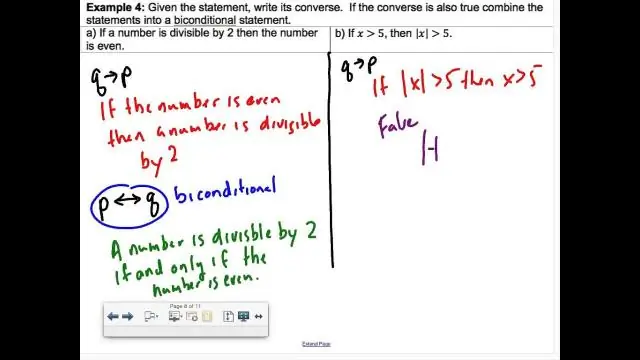
Tai yra dviejų sąlyginių teiginių derinys: „jei du linijos segmentai yra vienodi, jie yra vienodo ilgio“ir „jei du linijos atkarpos yra vienodo ilgio, tada jos yra sutapusios“. Dvi sąlyga yra teisinga tada ir tik tada, kai abi sąlygos yra teisingos. Dvigubos sąlygos žymimos simboliu ↔ arba ⇔
Kaip ką nors parašyti kaip funkciją?

Rašote funkcijas su funkcijos pavadinimu, po kurio nurodomas priklausomas kintamasis, pvz., f(x), g(x) arba net h(t), jei funkcija priklauso nuo laiko. Funkciją f(x) skaitote kaip „f iš x“, o h(t) – kaip „h iš t“. Funkcijos neturi būti tiesinės
