Turinys:
Video: Kaip rasti hiperbolės lygtį atsižvelgiant į asimptotus ir židinius?
2024 Autorius: Miles Stephen | [email protected]. Paskutinį kartą keistas: 2023-12-15 23:38
Remiantis aukščiau pateiktais argumentais, lygtys iš asimptotų yra y=±ab(x−h)+k y = ± a b (x − h) + k. Kaip hiperbolės sutelktas į kilmę, hiperbolės kurių centras yra taške (h, k), turi viršūnes, bendras viršūnes ir židiniai kurios yra susijusios su lygtis c2=a2+b2 c 2 = a 2 + b 2.
Atsižvelgiant į tai, kaip rasti asimptotės lygtį?
atlikdami šiuos veiksmus:
- Raskite asimptotų nuolydį. Hiperbolė yra vertikali, taigi asimptotų nuolydis yra.
- Naudokite 1 žingsnio nuolydį ir hiperbolės centrą kaip tašką, kad rastumėte lygties taško ir nuolydžio formą.
- Išspręskite y, kad rastumėte lygtį nuolydžio pertraukos forma.
Taip pat galima paklausti, kaip iš grafiko rasti hiperbolės lygtį? The lygtis turi formą y2a2−x2b2=1 y 2 a 2 − x 2 b 2 = 1, taigi skersinė ašis guli ant y ašies. The hiperbolė yra nukreiptas į pradžią, todėl viršūnės tarnauja kaip y-kirtimo taškai grafiką . Į rasti viršūnes, nustatykite x=0 x = 0 ir išspręskite y y.
Atitinkamai, kokia yra hiperbolės formulė?
Atstumas tarp židinių yra 2c. c2 = a2 + b2. kas hiperbolė turi du asimptotus. A hiperbolė su horizontalia skersine ašimi ir centru ties (h, k) turi vieną asimptotę su lygtis y = k + (x - h) o kitas su lygtis y = k - (x - h).
Kas yra B hiperbolėje?
Bendrojoje a lygtyje hiperbolė . a reiškia atstumą nuo viršūnės iki centro. b reiškia atstumą, statmeną skersinei ašiai, nuo viršūnės iki asimptotės linijos (-ių).
Rekomenduojamas:
Kaip rasti centrinį kampą atsižvelgiant į sektoriaus plotą ir spindulį?
Centrinio kampo nustatymas iš sektoriaus ploto (πr2) × (centrinis kampas laipsniais ÷ 360 laipsnių) = sektoriaus plotas. Jei centrinis kampas matuojamas radianais, formulė tampa tokia: sektoriaus plotas = r2 × (centrinis kampas radianais ÷ 2). (θ ÷ 360 laipsnių) × πr2. (52,3 ÷ 100 π) × 360. (52,3 ÷ 314) × 360
Kaip rasti vektoriaus komponentinę formą, atsižvelgiant į dydį ir kampą?
VIDEO Turint tai omenyje, ar 0 yra vieneto vektorius? A vieneto vektorius yra vektorius kurio dydis yra 1. Žymėjimas reiškia normą arba dydį vektorius v. Pagrindinis vienetiniai vektoriai ar aš = (1, 0 ) ir j = ( 0 , 1), kurių ilgis yra 1 ir kurių kryptys atitinkamai išilgai teigiamos x ir y ašies.
Kaip parašyti lygtį taško nuolydžio forma, atsižvelgiant į du taškus?
Yra įvairių formų, kuriomis galime parašyti tiesės lygtį: taško-nuolydžio forma, nuolydžio-kirtimo forma, standartine forma ir tt Tiesės lygtis su dviem taškais (x1, y1) ir (x2, y2) ), per kurią eina linija, yra pateikta taip: ((y - y1)/(x - x1)) / ((y2 - y1)/(x2 - x1))
Kaip rasti matmenis, atsižvelgiant į plotą ir perimetrą?
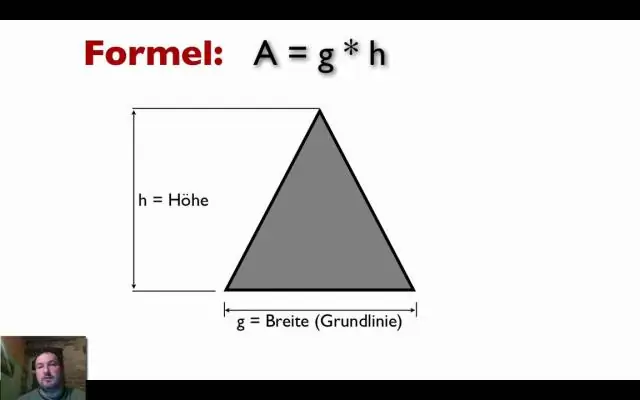
Ilgio ir pločio radimas, kai žinote plotą ir perimetrą Jei atsitiktinai žinote atstumą aplink stačiakampį, kuris yra jo perimetras, galite išspręsti L ir W lygčių porą. Pirmoji lygtis yra ta, kad plotui A = L ⋅ W, o antrasis – perimetrui P = 2L + 2W
Kaip rasti dėžutės aukštį, atsižvelgiant į paviršiaus plotą?
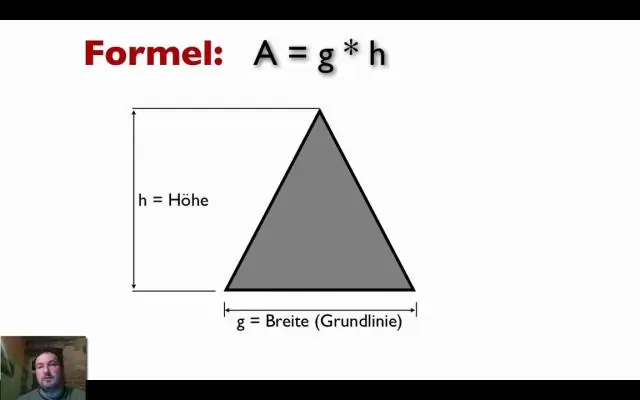
Sužinokite apie dėžutę Dėžutė dažniausiai apibūdinama pagal aukštį, plotį W ir ilgį L. Dėžės plotis, aukštis ir ilgis gali būti skirtingi. Tūris arba erdvės kiekis dėžutės viduje yra h × W × L. Išorinis dėžutės paviršiaus plotas yra 2 (h × W) + 2 (h × P) + 2 (W × P)