Video: Ar galite naudoti produkto taisyklę vietoj koeficiento taisyklės?
2024 Autorius: Miles Stephen | [email protected]. Paskutinį kartą keistas: 2023-12-15 23:38
Yra dvi priežastys, kodėl koeficiento taisyklė gali būti pranašesnis už valdžią taisyklė pliusas gaminio taisyklė skiriant a koeficientas : Supaprastinant rezultatą išsaugomi bendrieji vardikliai. Jeigu tu naudoji galia taisyklė plius gaminio taisyklė , tu dažnai reikia rasti bendrą vardiklį, kad rezultatas būtų supaprastintas.
Panašiai galima paklausti, kuo skiriasi produkto taisyklė ir koeficiento taisyklė?
The Produkto taisyklė sako, kad vedinys iš a produktas iš dviejų funkcijų yra pirmoji funkcija padauginta iš antrosios funkcijos išvestinės ir antroji funkcija padauginta iš pirmosios funkcijos išvestinė. The Produkto taisyklė turi būti naudojamas, kai išvestinė koeficientas reikia atlikti dvi funkcijas.
Taip pat žinote, kaip veikia produkto taisyklė? The gaminio taisyklė naudojamas skaičiavime, kai jūsų prašoma paimti išvestinę iš funkcijos, kuri yra poros ar kelių mažesnių funkcijų dauginimas. Kitaip tariant, funkcija f(x) yra a produktas funkcijų, jei ji gali parašyti kaip g(x)h(x) ir pan. Ši funkcija yra a produktas iš dviejų mažesnių funkcijų.
Kodėl tokiu būdu naudojame koeficiento taisyklę?
Įvadas į Dalinio taisyklė The koeficiento taisyklė yra paskutinė iš pagrindinių išvestinių finansinių priemonių apskaičiavimo taisyklių ir visų pirma susijusi su tuo, kas atsitiks, jei tu turėti funkciją, padalytą iš kitos funkcijos ir tu norėti imti to darinys.
Kokia yra koeficiento taisyklės formulė?
The koeficiento taisyklė yra formulę paėmus išvestinį a koeficientas dviejų funkcijų. The formulę teigia, kad norint rasti f(x) išvestinę, padalytą iš g(x), reikia: Paimti g(x) padauginus iš f(x) išvestinę. Tada iš to sandaugos turite atimti sandaugą iš f(x) padauginto iš g(x) išvestinės.
Rekomenduojamas:
Kaip naudojate sandaugos ir koeficiento taisyklę?
Produkto taisyklė sako, kad dviejų funkcijų sandaugos išvestinė yra pirmoji funkcija, padauginta iš antrosios funkcijos išvestinės ir antroji funkcija padauginta iš pirmosios funkcijos išvestinė. Produkto taisyklė turi būti naudojama, kai reikia paimti dviejų funkcijų koeficiento išvestinę
Kaip žinoti, kada naudoti produktą arba koeficiento taisyklę?
Funkcijų pasiskirstymas. Taigi, kai matote dviejų funkcijų dauginimą, naudokite sandaugos taisyklę, o dalybos atveju naudokite koeficiento taisyklę. Jei funkcija turi ir daugybą, ir padalijimą, tiesiog atitinkamai naudokite abi taisykles. Jei matote bendrąją lygtį, tai yra kažkas panašaus į ,, kur yra funkcija vien tik
Kuo skiriasi produkto taisyklė ir grandinės taisyklė?
Mes naudojame grandinės taisyklę, kai atskiriame „funkcijos funkciją“, pvz., f(g(x)) apskritai. Produkto taisyklę naudojame atskirdami dvi kartu padaugintas funkcijas, pvz., f(x)g(x) apskritai. Tačiau atminkite, kad tai yra atskiros funkcijos: viena nepasikliauja atsakymu į kitą
Kaip naudoti dešinės rankos taisyklę kryžminiam produktui?
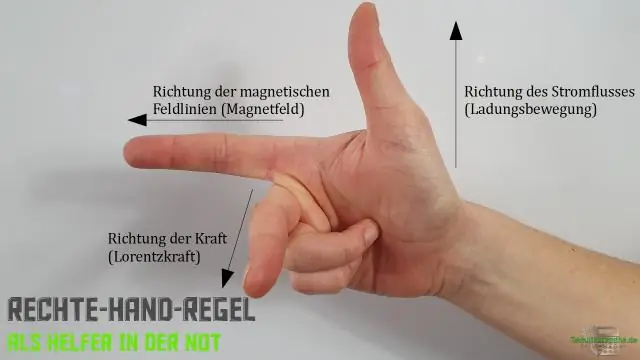
Dešiniosios rankos taisyklė teigia, kad vektorių kryžminės sandaugos orientacija nustatoma sudedant ir nuo uodegos iki uodegos, ištiesiant dešinę ranką, ištiesiant ją kryptimi, o paskui sulenkiant pirštus ta kryptimi, kuria daromas kampas. Tada nykštis rodo kryptimi
Kaip koeficiento taisyklę konvertuoti į produkto taisyklę?
Dalinio taisyklę galima vertinti kaip produkto ir grandinės taisyklių taikymą. Jei Q(x) = f(x)/g(x), tai Q(x) = f(x) * 1/(g(x)). Norėdami atskirti Q(x), galite naudoti produkto taisyklę, o 1/(g(x)) galima atskirti naudojant grandinės taisyklę, kai u = g(x) ir 1/(g(x)) = 1/u