
- Autorius Miles Stephen [email protected].
- Public 2023-12-15 23:38.
- Paskutinį kartą keistas 2025-01-22 17:04.
The apribojimas yra tai, kad vardiklis negali būti lygus nuliui. Taigi šioje užduotyje, kadangi 4x yra vardiklyje, jis negali būti lygus nuliui. Raskite visas x reikšmes, kurios vardiklyje yra nulis. Norėdami rasti apribojimai ant racionalus funkcija, suraskite kintamojo reikšmes, kurių vardiklis lygus 0.
Ar tokiu būdu racionali išraiška gali neturėti jokių apribojimų?
Na tas pats yra tiesa už racionalios išraiškos . Antras yra racionali išraiška vardiklyje niekada nėra nulio, todėl mes to nedarome reikia nerimauti bet kokius apribojimus . Taip pat atkreipkite dėmesį, kad antrojo skaitiklis racionalios išraiškos valia būti nuliui. Tai yra gerai, mes tiesiog reikia kad būtų išvengta padalijimo iš nulio.
Be to, kaip sprendžiate racionalias išraiškas? Racionalios lygties sprendimo žingsniai yra šie:
- Raskite bendrą vardiklį.
- Viską padauginkite iš bendro vardiklio.
- Supaprastinti.
- Patikrinkite atsakymą (-us), kad įsitikintumėte, jog nėra pašalinio sprendimo.
Antra, kodėl mes nustatome apribojimus racionaliai raiškai ir kada nurodome apribojimus?
Patvirtino atsakymą ekspertas Racionalios išraiškos yra tie, kurie turi trupmeninius terminus. Mes nurodome apribojimus nes dėl to kai kuriose x reikšmėse lygtis gali būti neapibrėžta. Dažniausiai racionalių posakių apribojimas yra N/0. Tai reiškia, kad bet koks skaičius, padalintas iš nulio, yra neapibrėžtas.
Kaip sprendžiate racionalias algebrines išraiškas?
- Sprendimas:
- 1 veiksmas: koeficientuokite visus vardiklius ir nustatykite LCD.
- 2 veiksmas: nustatykite apribojimus. Šiuo atveju jie yra x≠−2 x ≠ − 2 ir x≠−3 x ≠ − 3.
- 3 veiksmas: padauginkite abi lygties puses iš LCD.
- 4 veiksmas: išspręskite gautą lygtį.
- 5 veiksmas: patikrinkite, ar nėra pašalinių sprendimų.
Rekomenduojamas:
Kodėl mes nustatome apribojimus racionaliai raiškai ir kada nurodome apribojimus?

Nurodome apribojimus, nes dėl to kai kuriose x reikšmėse lygtis gali būti neapibrėžta. Dažniausias racionalių išraiškų apribojimas yra N/0. Tai reiškia, kad bet koks skaičius, padalintas iš nulio, yra neapibrėžtas. Pavyzdžiui, funkcijai f(x) = 6/x², pakeitus x=0, rezultatas būtų 6/0, kuris neapibrėžtas
Kaip AutoCAD taikyti matmenų apribojimus?
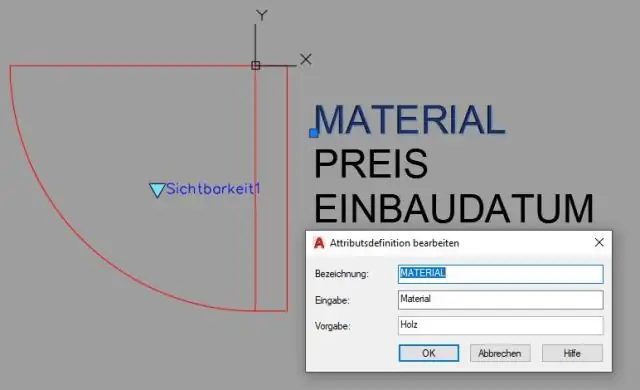
Šie veiksmai pateikia paprastą matmenų apribojimų pavyzdį: Pradėkite naują piešinį ir paverskite juostelės parametrų skirtuką aktualiu. Būsenos juostoje įjunkite atitinkamas tikslaus piešimo priemones, pvz., Snap, Ortho ir Osnap. Taikydami tikslią techniką, nubrėžkite pakankamai tikslią geometriją
Kuris teiginys geriausiai apibūdina neįtrauktas racionalios išraiškos reikšmes?

Neįtraukta racionalios išraiškos reikšmė yra tos reikšmės, kuriose išraiškos vardiklis yra nulis. Be to, polinomo nulių skaičius visada yra mažesnis arba lygus daugianario laipsniui. Vadinasi, neįtrauktų racionalios išraiškos reikšmių skaičius negali viršyti vardiklio laipsnio
Kokie yra racionalios algebrinės išraiškos dauginimo žingsniai?
Q ir S nėra lygūs 0. 1 veiksmas. Paskaičiuokite ir skaitiklį, ir vardiklį. 2 veiksmas: parašykite kaip vieną trupmeną. 3 veiksmas: supaprastinkite racionalią išraišką. 4 veiksmas: padauginkite visus likusius skaitiklio ir (arba) vardiklio veiksnius. 1 veiksmas: suskaičiuokite skaitiklį ir vardiklį. 2 veiksmas: parašykite kaip vieną trupmeną
Kas yra racionalios išraiškos apribojimas?

Apribojimas yra tas, kad vardiklis negali būti lygus nuliui. Taigi šioje užduotyje, kadangi 4x yra vardiklyje, jis negali būti lygus nuliui. Norėdami rasti racionalios funkcijos apribojimus, raskite kintamojo reikšmes, kurių vardiklis lygus 0
